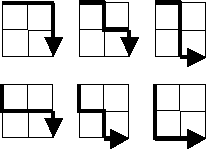
아래와 같은 2 × 2 격자의 왼쪽 위 모서리에서 출발하여 오른쪽 아래 모서리까지 도달하는 길은 모두 6가지가 있습니다 (거슬러 가지는 않기로 합니다).
그러면 20 × 20 격자에는 모두 몇 개의 경로가 있습니까?
순열.. 즉 흰바둑알20개, 검정바둑알20개를 일렬로 놓을 수 있는
경우의 수를 구하는 것으로 모델링이 된다고 한다.
결국, 40C20이므로 40!/20!*20! 로 수학공식화 가능함.
그냥 math.factorial 사용하면 되므로 코드는 skip!
It can indeed be solved in one equation, and curiously enough, the solution to it is in one of the other problems. The solution lies in the N choose R formula. For any number of rows R, you take (2R!)/(R! ^ 2). This comes from the equation n choose r = n!/r!(n-r)!, and you replace n with 2r, for the number of rows problem. :)
위 내용이 좀 참고가 될듯~~
결국 우측-R, 아래-D로 놓고 보면
RRDD
RDRD
DRDR
DDRR
DRRD
RDDR
형태가 되기 때문에 ...
for a generalized solution of gridsize n*n, routes= [(2n)!]/[n!*n!] 이런 공식으로 풀리는듯...
루비로 다른 방식의 풀이된 코드가 있어 공유..